Exhaustively testing a randomized blackbox interpreter

April 28, 2021

Suppose you have a black box interpreter that runs some programming language. The interpreter is allowed to have some randomness, but it’s entirely supplied by a give_me_a_random_number function that you pass into it. How do we exhaustively test and enumerate all possible execution paths?

Premise

Recently for uWaterloo’s CS 442 class, I had to write an interpreter for a toy language. It was a very simple Object Oriented language with basic support for concurrency. Since it was inspired by pi-calculus, naturally there is some nondeterminism. For example, consider 3 processes. If process 1 wants to send value foo, and process 2 and 3 both want to receive it, who should get it?

The possible concurrent steps in the language were:

  1. spawn: spawns a new process
  2. send/receive: send/receive a message over a channel
    • e.g. send("channel_name", foo) sends foo to some process that is waiting to receive via receive("channel_name", &bar)

The way we ran the interpreter was as follows:

  1. run all the non-concurrent steps of each process (i.e. run process 1 until we reach a concurrent step, then do the same for processes 2, 3, etc..)
  2. out of all the concurrent steps, choose one using a given function (randomizer: int -> int)
    • say we have n concurrent steps to choose from. Then randomizer(n) returns a number i in (0, 1, ..., n-1), so we’d do the ith concurrent step
  3. repeat until finished

The interpreter itself wasn’t too hard to write, but I was confused - how will the instructor test this, considering tons of programs would be nondeterministic? There was no restriction on how we ordered processes, so even providing a deterministic “randomizer” like (fun _ -> 0) wouldn’t guarantee some expected output across all students’ implementations.

My teacher (Professor Richards) noted that for small programs, it’s feasible to enumerate all possible outputs by running the program repeatedly and filling in an execution tree. This inspired me to try my hand at testing the interpreter as a black box.

What’s the “execution tree”?

Consider the following pseudocode:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

def main():
    spawn(Foo)
    spawn(Bar)
    spawn(Baz)

class Foo:
    def main():
        spawn(Baz)

class Bar:
    def main():
        spawn(Baz)

class Baz:
    def main():
        print("1")

We start with a singleton list of processes, in particular the main() function at line 1. Let’s represent this with [1]. At line 2, we spawn a new process which goes to Foo::main(). Then, we’re stuck between two concurrent steps: [3, 8]. Namely, should I spawn a Bar in line 3 or should I spawn a Baz in line 8? We solve this using a randomizer(2) call, which helps us decide.

If we choose to run step 3, then we eventually get stuck at [4, 8, 12].

If we choose to run step 8, then we eventually get stuck at [3, 12].

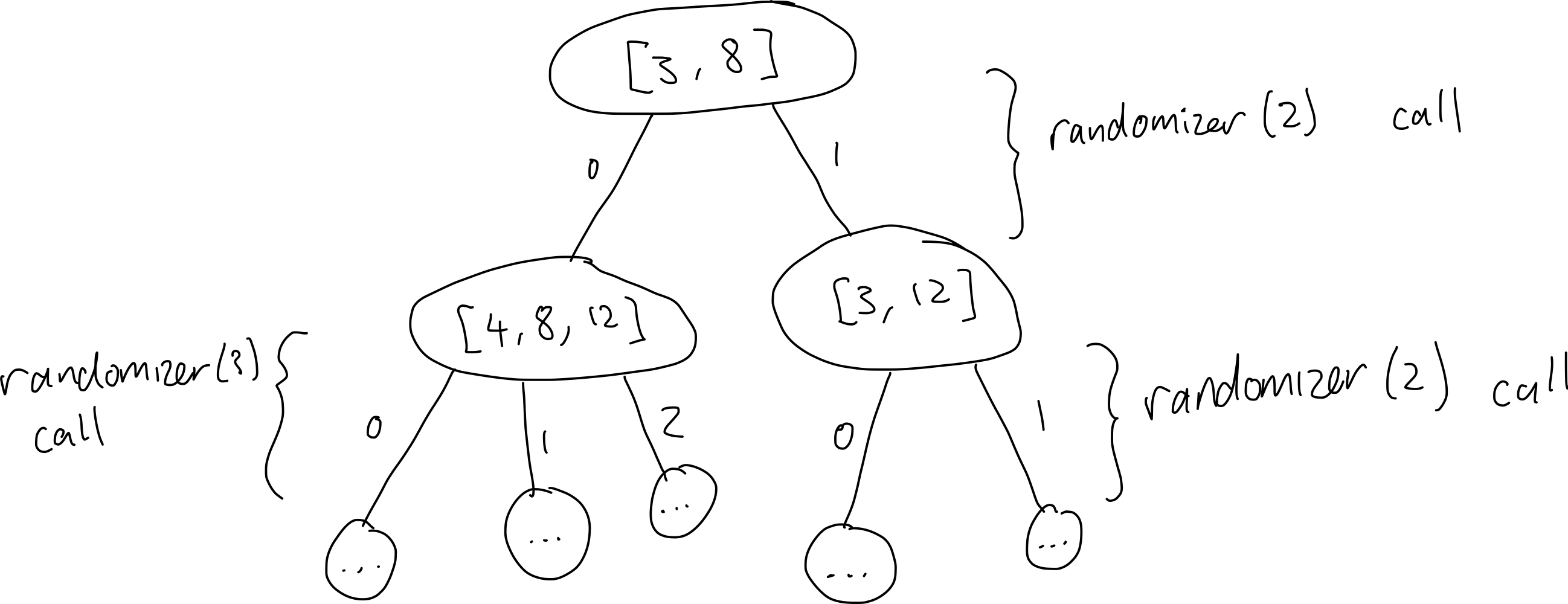
execution tree
Figure 1 - A simple execution tree for the pseudocode, truncated at depth 2

Now we note a few things:

Given this, notice that we can dynamically build up an execution tree to enumerate all possible executions. Every randomizer(n) call is a “branch point” with n different children. We simply need to pass in a custom randomizer function that helps us keep track of state on every call!

Iteratively building and pruning

First, we define a type for the execution tree.

type t =
  | Unexplored
  | Done
  | Node of t ref list
;;

Since we’ll need to dynamically change nodes, I chose to keep track of children with t ref’s (kind of like a pointer, if you’re not used to OCaml). Then it will be simple for me to change a given Node’s child.

Then, we keep some global state that the randomizer updates.

let cur = ref (ref Unexplored)

We hold an invariant throughout every run that before a randomizer call, the cur variable points to the node in the execution tree that the program is currently in. For example, on a fresh run we should start with cur pointing to the root (i.e. Main). Then if we return 0 from a randomizer call, the program descends to the 0’th child and so we should update cur to point to that node. Then we can use the randomizer to build the tree as follows.

On a randomizer(n) call:

You might ask “what if we go to a Done node?”. In this case, we have made a mistake because we’re essentially following a path that we have already fully explored. This is also true for the case where we arrive at a Node with the children all being Done. To avoid these mistakes, we simply prune the tree every time before we run the program.

In code form, it looks like this:

let randomizer (n: int) : int =
  if n = 1 then 0
  else (
    match ! ! cur with
    | Done -> failwith "this should never happen"
    | Unexplored ->
      let children = (List.init n ~f:(fun _ -> ref Unexplored)) in
      !cur := Node children;
      cur := (List.nth_exn children 0);
      0
    | Node children ->
      match
        List.findi children
          ~f:(fun _ t -> match !t with Done -> false | _ -> true)
      with
      | None -> failwith "this should never happen"
      | Some (i, child) ->
        cur := child;
        i
  )
;;

Now we can iteratively build the tree by repeatedly running the program. First, we prune the tree by removing any fully explored paths. Then we set the cur to point to root, and run. After a run, we know we’ve fully explored one of the paths, so we set the leaf node that cur points to to be Done. We repeat the process, iteratively building a tree and pruning it until we are left with a root node which is also Done.

The code for this:

let rec prune_tree (node : t ref) : unit =
  match !node with
  | Unexplored -> ()
  | Done -> ()
  | Node children ->
    List.iter children ~f:prune_tree;
    if List.for_all children ~f:(fun child ->
        match !child with
        | Done -> true
        | _ -> false)
    then node := Done
;;

let run (prog : string) : unit  =
  let root = ref Unexplored in
  let rec run () =
    prune_tree root;
    match !root with
    | Done -> ()
    | _ ->
      print_endline "RUNNING:";
      cur := root;
      Interpreter.run_program ~randomizer prog |> Or_error.ok_exn;
      !cur := Done;
      run ()
  in
  run ()
;;

An example

This could be confusing, so I made an illustration to showcase the core logic.

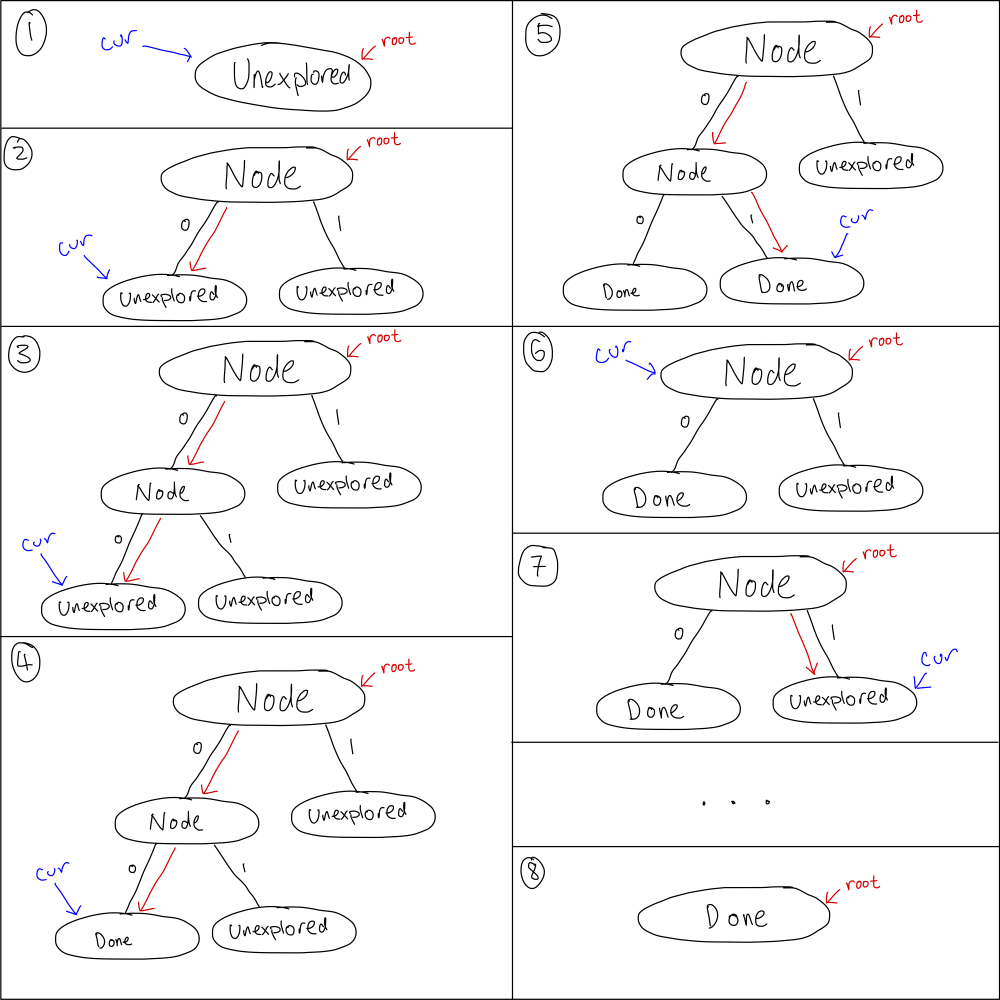
sample runthrough
Figure 2 - A sample runthrough of the program
  1. We start with a root node of Unexplored
  2. We run the program, until we get a randomizer(2) call. Then we update the root to now be a Node with 2 unexplored children. We update the cur pointer to the 0th child, and we return 0 from the randomizer call.
  3. Similar to 2
  4. We’re now done an execution of the program. We update the leaf node that cur is pointing at to be Done
  5. We restart, but this time going down a different path
  6. We prune the tree
  7. We restart, going down a different path
  8. We continue this until we eventually prune the tree to be a singular Done node

Conclusion

That’s it! By updating some global state on every randomizer call, we can enumerate all possible paths of execution. As a result, for small programs its feasible generate all possible outputs. Now it’s possible to test that two different interpreters indeed do the same thing for a program, even if the program has some nondeterminisim in it!

Note: By small program, I mean small interns of “branch points”, not LoC. Even a very low LoC program could cause $O($a lot$)$ of work.

SOCIALS